Activité 2 : SE REPERER SUR TERRE
Dans sa ville portuaire dite Saint-Nazaire Léo rêve de voyage. Ainsi, il pense à son correspondant espagnol, Manolo, qui vit à Cuenca. Il songe aussi à son cousin Pierre, qui est parti en voyage scolaire linguistique à Constance en Allemagne. La mère de Léo, quant à elle, est partie en voyage professionnel à Seattle aux USA.
A cette occasion, nous pourrons nous demander comment calculer et comparer certaines longueurs de la Terre ?
Quelle coordonnée, longitude ou latitude, partage Léo en première approximation avec chacune des villes de Cuenca et Constance quand il est à Saint Nazaire ?
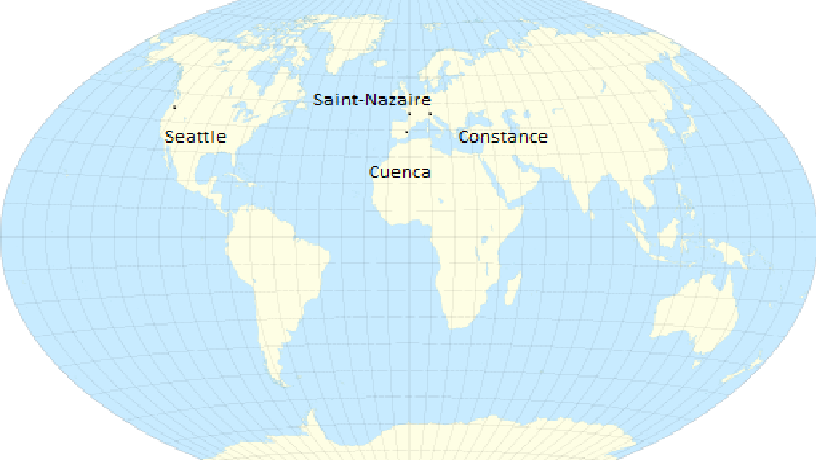
Les coordonnées partagées sont la latitude entre Saint-Nazaire (47°16) et Constance (47°40) et la longitude entre Saint-Nazaire (2°12) et Cuenca (2°07).
Lequel des deux amis, Manolo ou Pierre, est le plus proche de Léo ?
- Formule : mAB = r × θ
- Rayon terrestre : R = 6366 km
- Conversion en degrés :
- Latitude Saint-Nazaire: 47 + 16/60 = 47.267°
- Longitude Saint-Nazaire: -2 - 12/60 = -2,2°
- Latitude Cuenca: 40 + 4/60 = 40,067°
- Longitude Cuenca: -2 - 7/60 = −2,117°
- Conversion en radians :
- Latitude Saint-Nazaire: 47,267 × π/180 = 0,825 radians
- Longitude Saint-Nazaire: -2,2 × π/180 = -0,038 radians
- Latitude Cuenca: 40,067 × π/180 = 0,7 radians
- Longitude Cuenca: -2,117 × π/180 = -0,037 radians
- Calcul de Δ∅ et ΔL :
- Δ∅ = 0,825 - 0,7 = 0,125 radians
- ΔL = -0,038 - (-0,037) = -0,001 radians
- Calcul de θ : θ = √((Δ∅)² + (ΔL)²) = 0.125 radians
- Calcul de r : r = cos((∅Saint-Nazaire +∅Cuenca)/2) × R → r ≈ 4603 km
- Distance : mSaintNazaire-Cuenca ≈ 4603 × 0,125 ≈ 575,42 km
- Distance Saint-Nazaire-Constance ≈ 854,3 km
- Distance Saint-Nazaire-Seattle ≈ 9033,86 km
- Explication de calcul :
- Conclusion :
- Conversion en degrés :
- Latitude Saint-Nazaire: 47 + 16/60 = 47.267°
- Longitude Saint-Nazaire: -2 - 12/60 = -2.2°
- Latitude Seattle: 47 + 37/60 = 47,62°
- Longitude Seattle: -122 - 20/60 = −122,33°
- Conversion en radians :
- Latitude Saint-Nazaire: 47.267 × π/180 = 0,825 radians
- Longitude Saint-Nazaire: -2.2 × π/180 = -0,038 radians
- Latitude Seattle: 47,62 × π/180 = 0,83 radians
- Longitude Seattle: −122,33 × π/180 = -2,135 radians
- Calcul de Δ∅ et ΔL :
- Δ∅ = 0,825 - 0,83 = -0,005 radians
- ΔL = -0,038 - (-2,135) = 2,097 radians
- Calcul de θ : θ = √((Δ∅)² + (ΔL)²) = 2,097 radians
- Calcul de r : r = cos((∅Saint-Nazaire +∅Seattle)/2) × R → r ≈ 4308 km
- Distance : mSaintNazaire-Cuenca ≈ 4603 × 0.125 ≈ 9033,86 km
En suivant une démarche similaire :
Nous avons d'abord converti les coordonnées en radians avec la relation angle × π/180 = radians car P = 2 π × R et la terre est un sphere donc il faut calculer en radians, ensuite on a calculé theta θ qui vaut la valeur absolue de Δ∅ et ΔL.
Puisque la terre n'est pas un sphere parfait nous avons utilisé la relation r = cos(∅) × R pour calculer son rayon en foction de son altitude, ce qui sera utilisé ensuite pour calculer la distance entre deux points sur la terre avec la relation mAB = r × θ
La figure intéractive ci-dessous peut démontrer la relation (r = cos(∅) × R) entre la latitude et le rayon de la Terre:
Manolo(Cuenca) est plus proche de Léo(Saint-Nazaire) que Pierre(Constance).
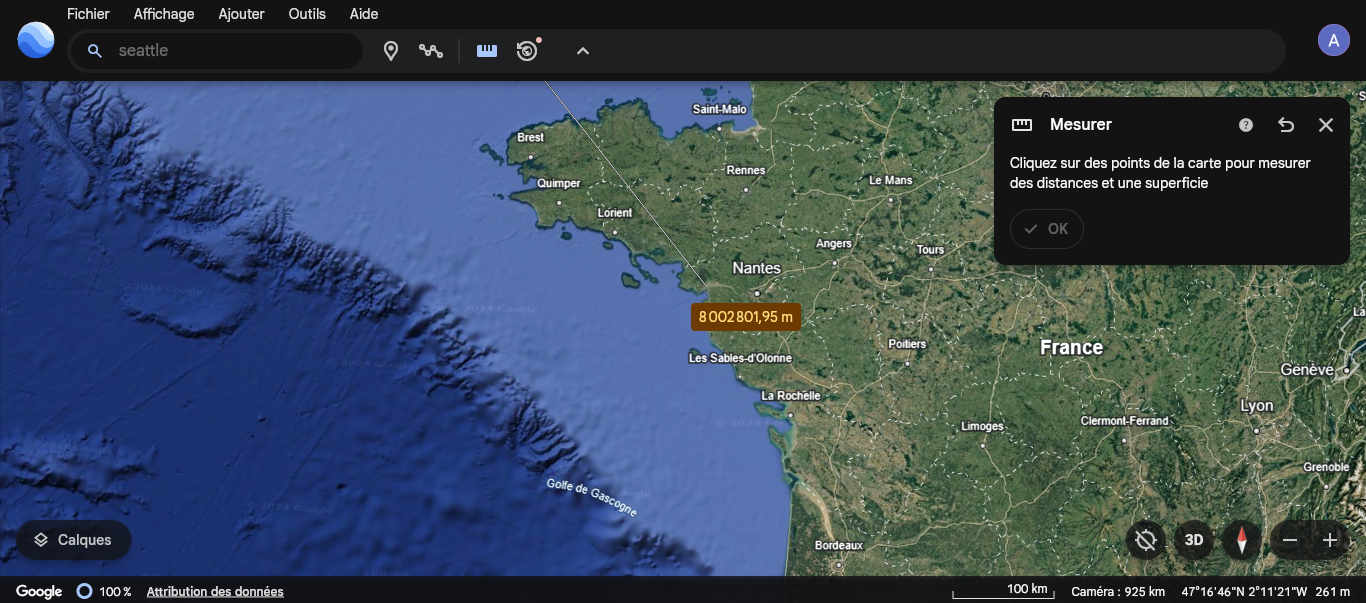
Calculez la longueur de l’arc de parallèle qui sépare Léo de sa mère. En utilisant un système d’information géographique tel que Google Earth, précisez s’il s’agit du chemin le plus court pour aller à Seattle.
On peut donc déduire à partir du résultat du calcul et le résultat de Google Earth que non, cela ne s'agit pas du chemin le plus court